介绍

快排是对冒泡排序的一种改进，是非常重要且高效的排序算法，其平均复杂度为O(nlogn)，最坏条件O(n^2)

思路

通过多次比较和交换来实现排序，在一趟排序中把将要排序的数据分成两个独立的部分，对这两部分进行排序使得其中一部分所有数据比另一部分小，然后继续递归排序，最终实现所有数据有序。

大致步骤：

1. 设置一个分界线也就是基准值，通过该分界线将数据分成两部分。
2. 将大于或等于分界值的数据集中到右边，小于分界值的数据集中到左边。一趟排序过后，左边部分中各个数据元素都小于分界值，而右边部分中各数据元素都大于或等于分界值，且右边部分个数据元素皆大于左边所有数据元素。
3. 然后，左边和右边的数据可以看成两组不同的部分，重复上述1和2步骤
   当左右两部分都有序时，整个数据就完成了排序。

图解

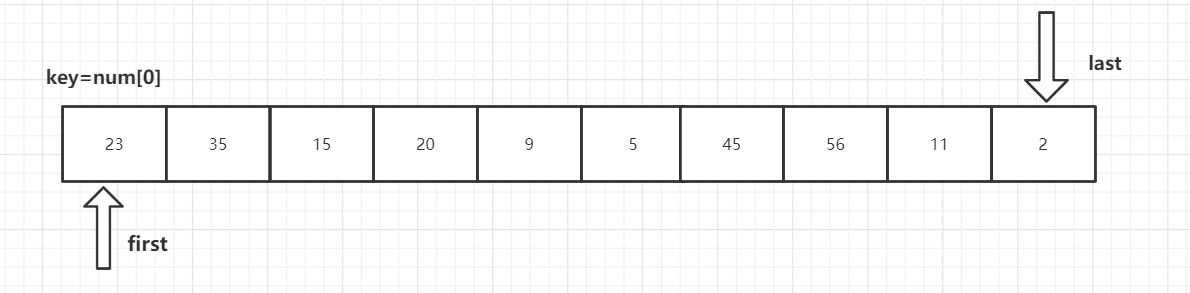
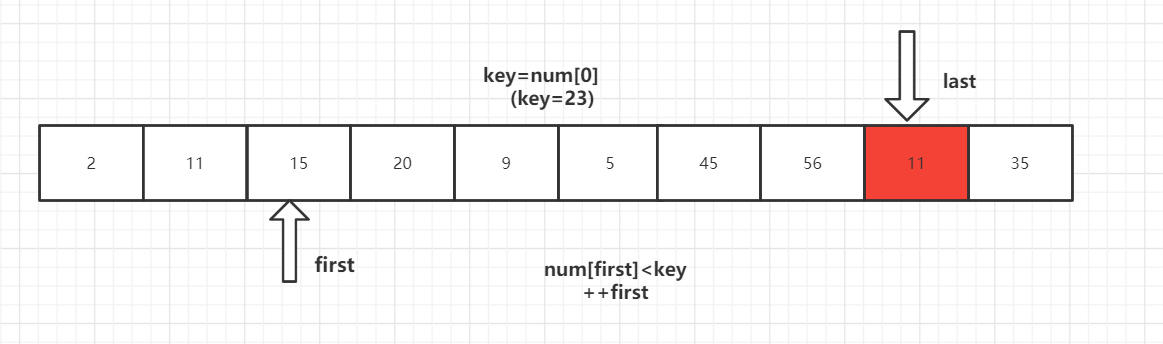
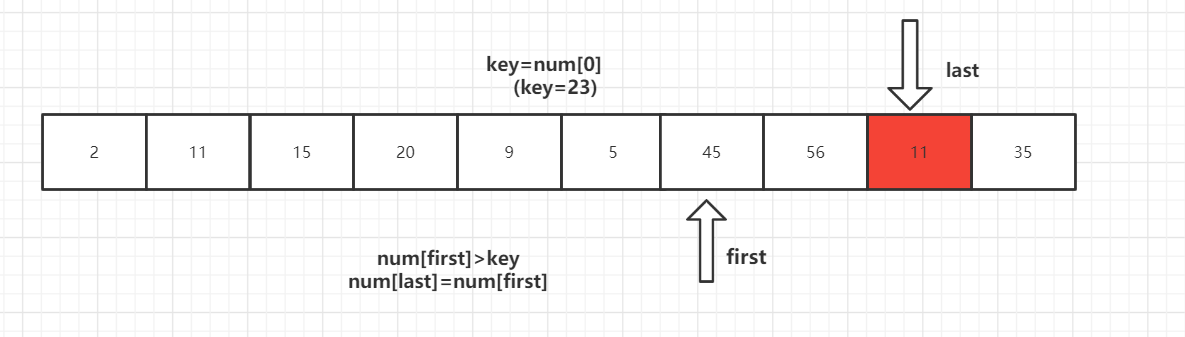
首先设置三个参数，first指向区间左端，last指向区间右端，key为当前的分界值。
从待排序的数据元素中选取一个通常为第一个作为基准值元素（key）key=num[0]，设置双指针first指向区间左端，last指向区间右端。

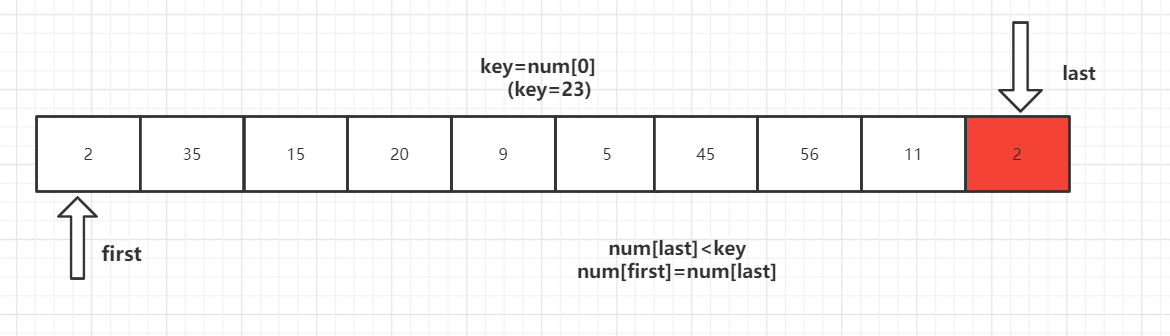
第一步：
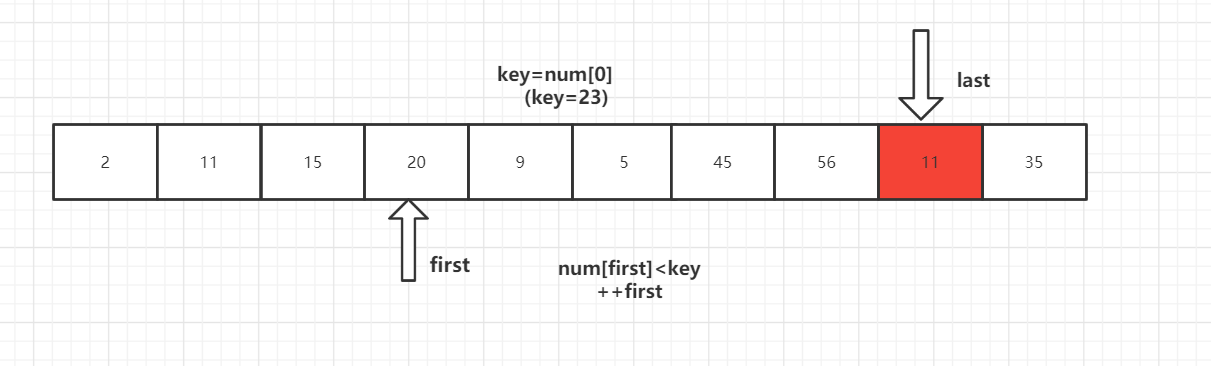
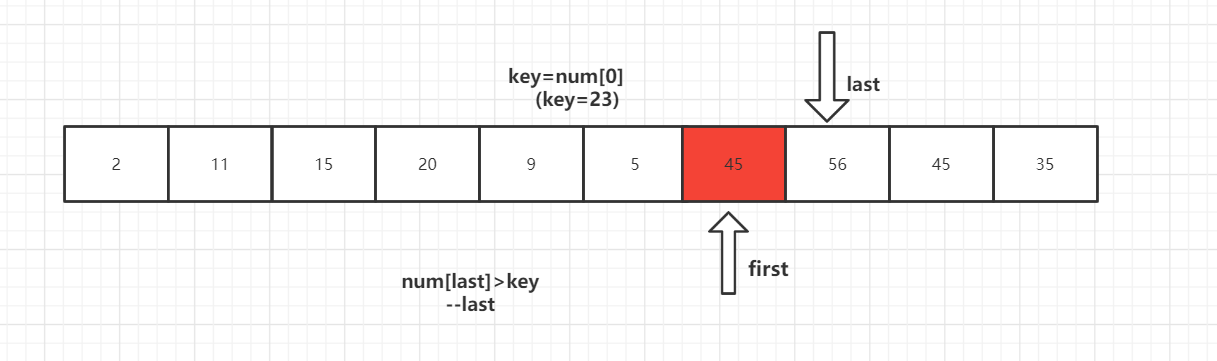
key 首先与 num[last] 进行比较，如果 num[last]<key，则num[first]=num[last]将这个比key小的数放到左边去，如果num[last]>=key则- -last，再拿num[last]与key进行比较，直到num[last]<key交换元素为止。

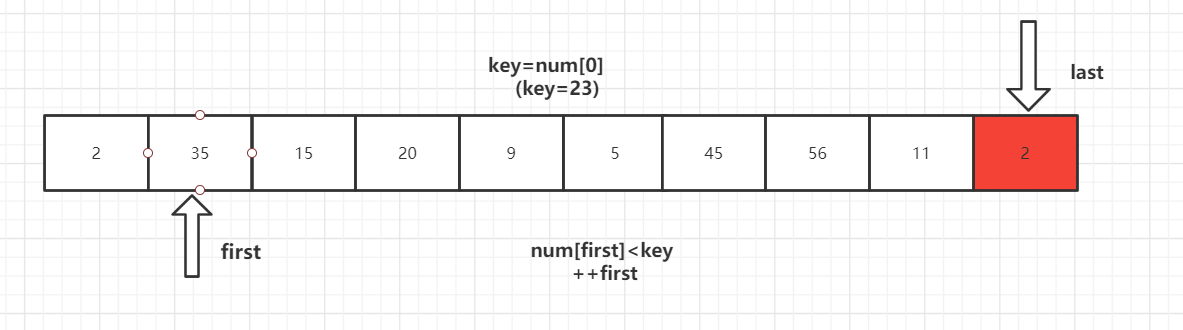
第二步：
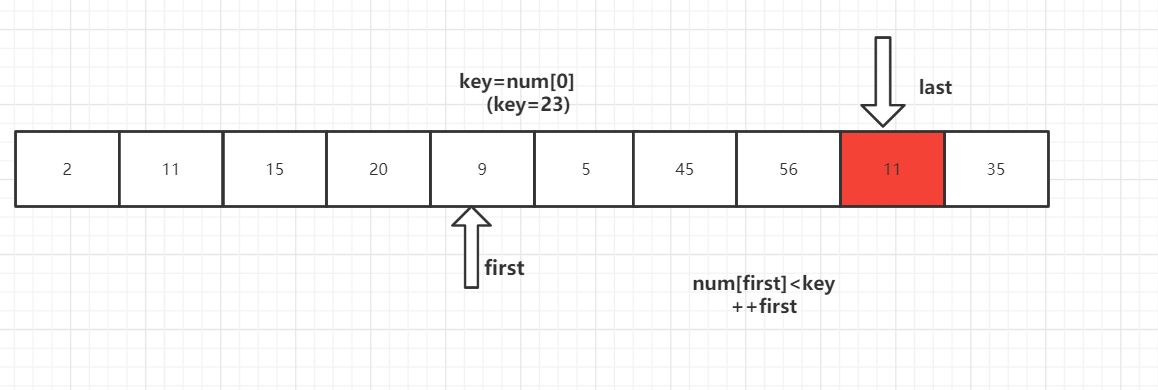
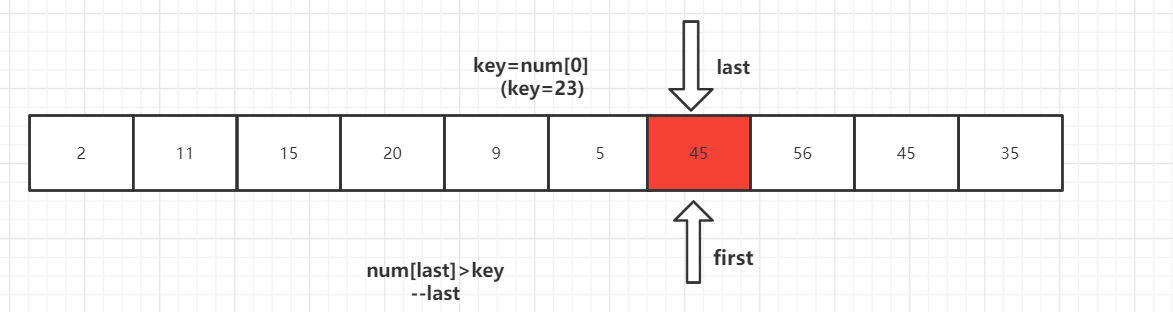
num[last]<key交换元素后，转向左边部分，用num[first]与key进行比较，如果num[first]<key,则++first，然后继续进行比较，直至num[first]>key,则将num[last]=num[first]。


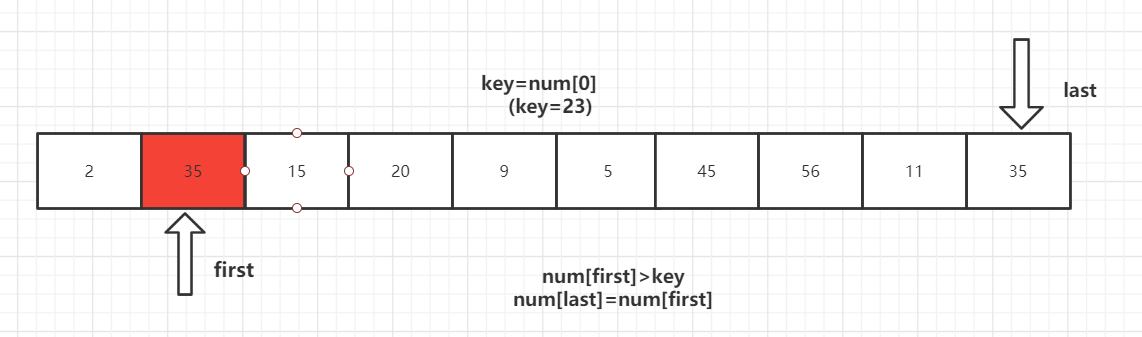
第三步：
重复上述操作








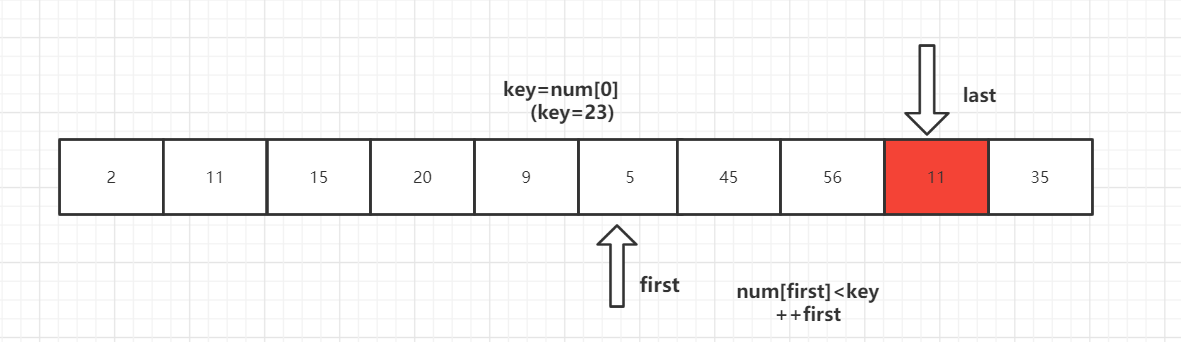
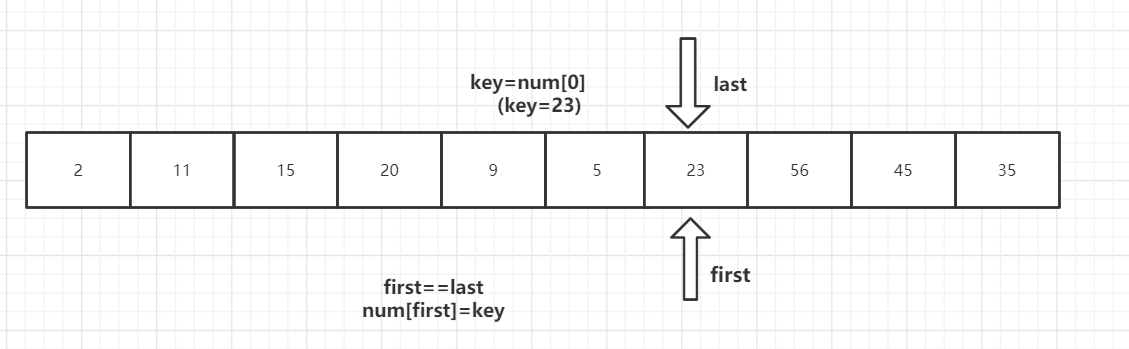
第四步：
第一趟结束，得到[2,11,15,20,9,5]23[56,45,35]
然后对左子列和右子列进行同样操作
2 [11,15,20,9,5] 23 [35,45] 56
2 [5,9] 11 [20,15] 23 35 45 56
2 5 9 11 15 20 23 35 45 56

算法分析

每次数据元素都能平均的分成两个部分。得到一个完全二叉树。如果有n个数据元素，那么数的深度为[log2(n)]+1,时间复杂度为O(nlogn)
在最坏条件下，仅有左子树或右子树为n*(n-1)/2时间复杂度为O(n^2),在待排序数组已经有序的情况下复杂度最高
空间复杂度为O(n)
快速排序是一种不稳定的排序算法，会改变数据元素的相对位置，也是内排序中平均效率最高的排序算法。

代码

javascript

var quicksort = function (num, l, r) {
    //r为数组元素总个数，last下标等于r-1
    let first = l;
    let last = r - 1;
    let key = num[first];
    while (first < last) {
        while (first < last && num[last] >= key) {
            last--;
        }
        //如果值小于 key分界值 交换
        num[first] = num[last];
        while (first < last && num[first] < key) {
            first++;
        }
        //如果值大于key分界值 交换
        num[last] = num[first];
    }
    num[first] = key;
    //递归左右部分进行快排
    if (first > l) {
        num = quicksort(num, l, first);
    }
    if (first + 1 < r) {
        num = quicksort(num, first + 1, r);
    }
    return num;
};

go

func quicksort(num []int, l, r int) []int {
	//r为数组元素总个数，last下标等于r-1
	first := l
	last := r - 1
	key := num[first]
	for first < last {
		for first < last && num[last] >= key {
			last--
		}
		//如果值小于 key分界值 交换
		num[first] = num[last]
		for first < last && num[first] < key {
			first++
		}
		//如果值大于key分界值 交换
		num[last] = num[first]
	}
	num[first] = key
	//递归左右部分进行快排
	if first > l {
		num = quicksort(num, l, first)
	}
	if first+1 < r {
		num = quicksort(num, first+1, r)
	}
	return num
}

原文链接：https://blog.csdn.net/qq_52595134/article/details/118943109

Q.E.D.